Modifiable Area Unit Problem (MAUP)

MAUP: THE MODIFIABLE AREA UNIT PROBLEM

DOTS TO BOXES: DO THE SIZE AND SHAPE OF SPATIAL UNITS JEOPARDIZE ECONOMIC GEOGRAPHY ESTIMATIONS?

A.      Briant, P. P. Combes & B. Lafourcade, Journal of Urban Economics, 67 2010)

(Notes from Lecture, Problem set and above referenced paper) 

MAUP

The Modifiable Area Unit Problem (MAUP) arises when working with statistical data, and is concerned with the sensitivity of results to the particular choice of zoning system that is used in the analysis. The core of the problem is that we often do not know how driven our statistical results are by the shape/size of the areas under examination and how data within those areas have been aggregated. As the paper shows, coefficients can vary depending on how data are aggregated within different area units.

For example when examining the effects of agglomeration on regional economies, it is often unclear whether results are truly driven by knowledge spillovers, labour pooling effects etc. or whether results are simply the product of how the data are organized. This is an important issue when thinking about policy regarding cluster formation strategies. When investigating such economic processes that have spatial characteristics, results will be affected by shape/size of the clusters used, when those clusters do not accurately reflect the underlying economic realities. Put another way, if data are generate by a particular spatial process, results of analysis will be affected when the units employed do not reflect the underlying data process. Returning to the agglomeration example, if the units of analysis are not well chosen then the zones will pick up/fail to pick up the effects of industries not-in/in their true field of economic influence. This will then tend to over/understate the effects on agglomerations on economic outcomes.

 

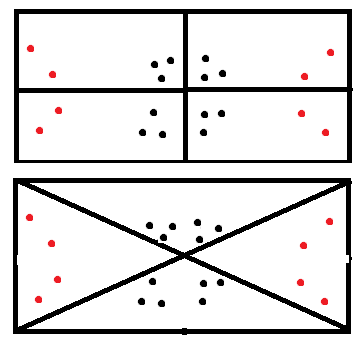
The shape effect refers to results that are driven by different shapes used in analysis. In the boxes, if a black dot is skilled labour productivity and the red is unskilled, then we see even distribution of productivity in the top panel. However, redrawing the shape means that we identify two clusters of high productivity workers, and two clusters of low productivity workers.

 

The size effect refers to the size of the units. I have not drawn an example but it is easy to see that using smaller triangles may find smaller less dense clusters of high productivity areas, and similarly clustered low productivity areas.

 

Illustrations with Simulated Data

Arbia (1989) says that the problems of shape and size distortion are minimized (not eliminated) when there is exact equivalence of sub-area (in terms of size and area), and there is an absence of spatial autocorrelation. In practice these two restrictions will very rarely be met. With regard to the lack of spatial correlation, this will rarely be the case as there are likely to be spillover effects from activities or outcomes or processes in one area upon another.

 

Amrhein (1995) simulated data by randomly generated variables and randomly assigning them to a Cartesian address (i.e. no autocorrelation). He then varied the unit size to 100, 49 and 9 squares of observation. Under these conditions he was able to show that means do not show any particular sensitivity to shape/size effects, although variances increase (and hence standard errors) as the sample size decreases (i.e. when moving to a smaller number of units).

 

Amrhein & Reynolds (1997) then went on to show that distortions using real census data were sensitive to both shape and size effects but also the aggregation process (i.e. whether data are summed or averaged). It is fairly intuitive to understand this. If data are aggregated by summation, they will be more distorted by an increase in size (as more observations are added) than averaging (the effect of adding more observations is reduced due to the effect of averaging).

 

Correlation Distortions

The MAUP can produce distortions in multivariate analysis of data drawn from spatial units. The effects of shape/size and the effects of aggregation have been separated out. Amrhein (1995) finds that his coefficients are sensitive both to size and shape, but if the model is well specified the method of aggregation seems to imply fewer distortions. When aggregation affects the dependent and dependent variable in the same way, the effects are small, and this goes for the shape effects also. However, when they are aggregated differently, they will not have the same degree of spatial autocorrelation and hence the size etc. effects will be larger.

 

Thus the problem is likely to be smaller for wage regressions (where data are averaged) than for gravity regressions (where data are summed).

 

Testing the Problem

The authors look at the effects of employment density on wage levels in France using a variety of different zoning methods. Specifically they use

• 341 Employment areas – government units based on minimizing daily commute between zones.
• 21 Regions
• 94 departments
• 22 Large squares
• 91 medium squares
• 341 small squares
• 100 semi-random zones.

Some of the data are summed (employment/trade flows) whereas some are averaged (wage rates); the former increase with the size of the units, whereas the latter are relatively more stable across different zoning systems.

 

The first thing they do is to calculate the Gini coefficients within every zoning system for the 98 industries examined throughout 18 years and rank them. Using rank correlation analysis they show that the ranking of industries is virtually unaffected by changes in zoning system. However when they use different indexes (e.g. Ellison and Glaeser indices) to rank the industries the rank coefficients are lower meaning that MAUP problems are more pronounced when using alternate indices. This indicates that the index rather than the MAUP is a more significant problem, and thus careful specification of index used should be a more primary concern than issues to do with units of observation.

 

They then undertake basic regression analysis of log wages on log employment density and a vector of controls. They find that the effects of moving from one zoning system to another are generally small. This is so especially when moving from very small to slightly less small units. The grid system is generally more sensitive which indicates that boundaries that do not reflect administrative/economic realities do generate more error. However, when they control for observed and unobserved skill levels (in order to see if workers are sorting into high density employment areas) the coefficient on density changes by an order of magnitude more than it did for changes due to MAUP. Thus, specification of the model again appears to be significantly more important than MAUP.

 

Similar changes are observed when market potential (measured as distance to other employment centres) and different definitions of market potential are controlled for. These changes to specification are all more important than MAUP.

 

Lastly they look at gravity equations for which the dependent variable (trade flows) are summed within zones, and these summations make the coefficients more sensitive to MAUP problems.